Bitwise Operations
Bitwise operations are a set of operations on binary strings (also known as bit strings) that will evaluate and manipulate individual bits of their inputs sequentially. These operators are implemented in most high level programming languages and CPU instruction set architectures, having a wide range of use cases and being incredibly important for manipulating data at the bit level. Here, we will cover the most notable bitwise operators, explaining how they work and their applications.
Bitwise AND
Provided two equal length bit strings, the bitwise AND will perform the logical AND on each bit in the bit strings. For each bit position, if both binary strings contain a 1 in that position, AND will return a 1. Otherwise, AND returns 0 in that position.
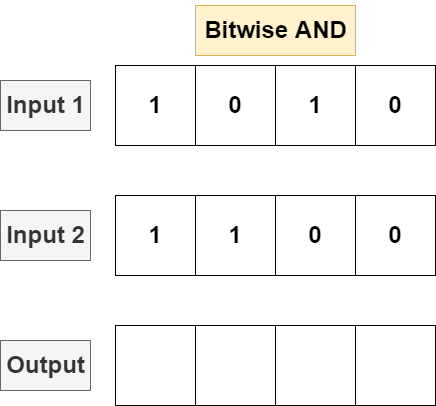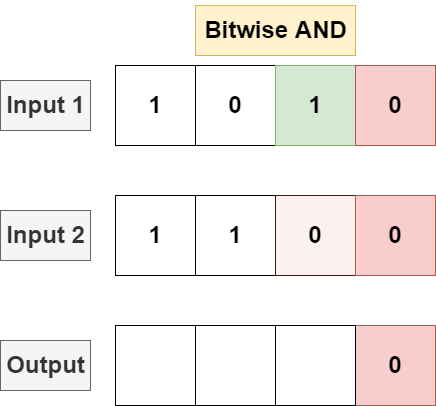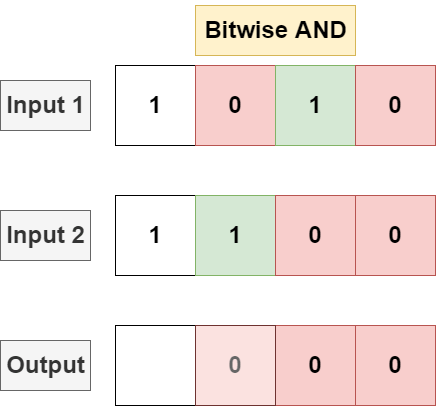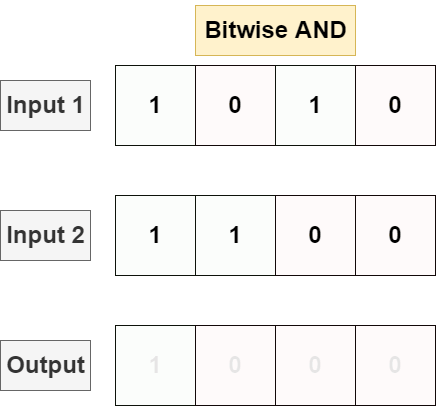
Programming languages will typically implement bitwise AND with the & operator (distinct from &&) which supports operations over integers. Consider the following Python snippet:
a = 0b100 # 4 represented in binary
b = 0b110 # 6 represented in binary
print(bin(a & b))0b100
Bitwise OR
Bitwise OR will perform logical OR on each bit, returning 1 if there is a 1 in either input for each bit position, returning 0 otherwise.
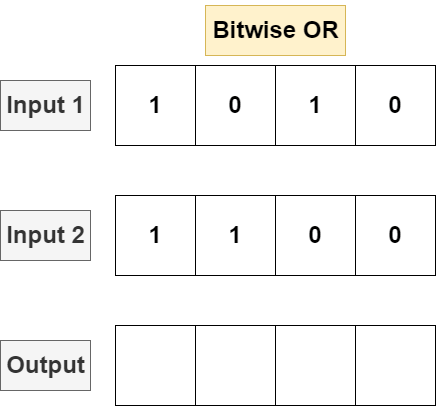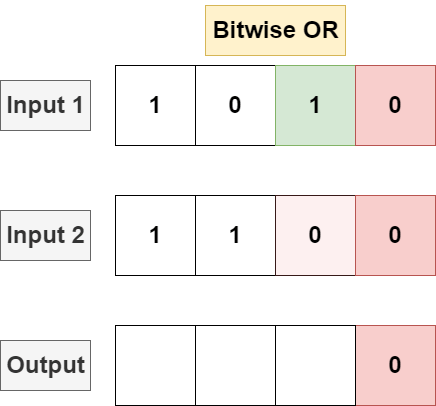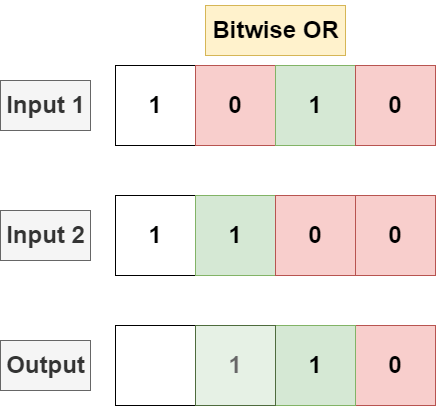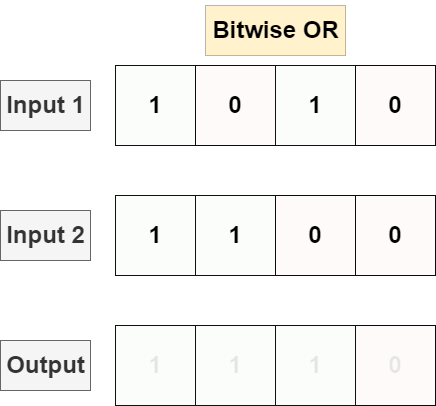
Languages typically implement OR with the | operator (distinct from ||) used on integer operations:
a = 0b100
b = 0b110
print(bin(a | b))0b110
Bitwise XOR
XOR will perform a logical XOR on each bit, returning 1 if one and only one input contains a 1 in a position, returning 0 otherwise.
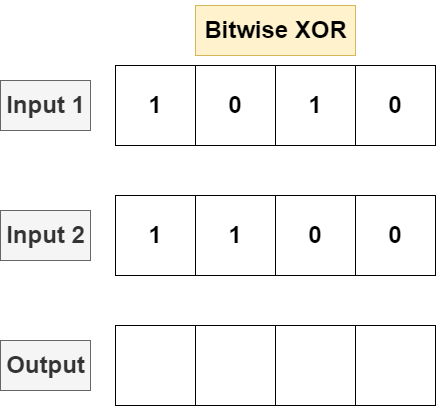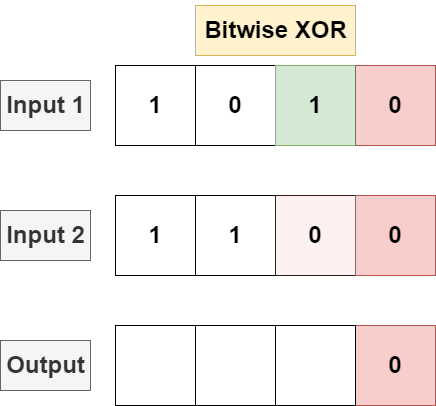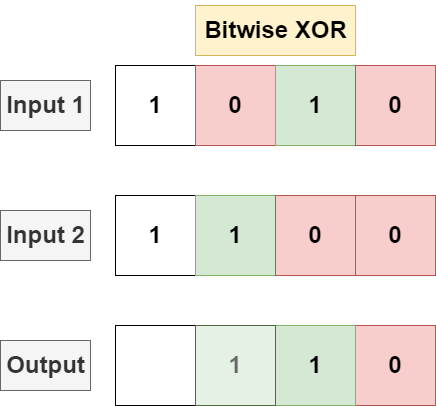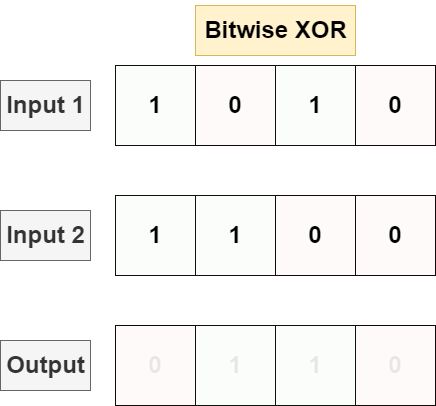
XOR is implemented with the ^ operator in most languages:
a = 0b100
b = 0b110
print(bin(a ^ b))0b10
Bitwise NOT
Given a single input bitstring, bitwise NOT will invert every single bit in the bit string, flipping each 1 to a 0 and vice versa.
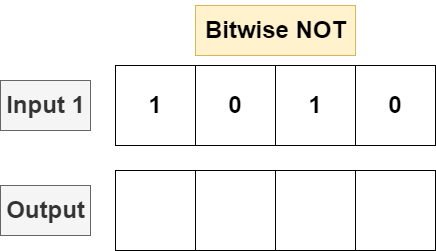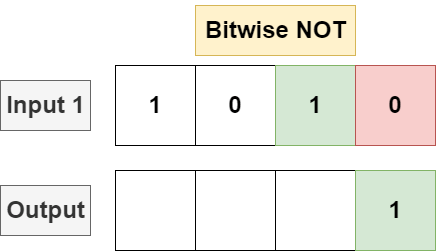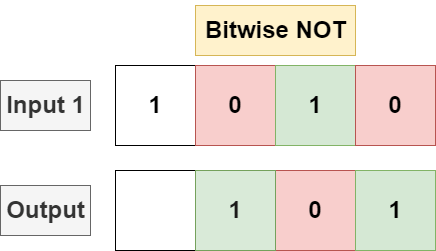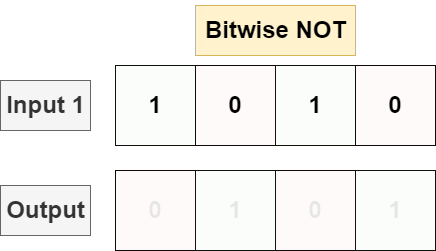
Programming languages typically implement NOT with the ~ operator:
a = 0b100
print(bin(~a))0b011
Bit shifting
Most programming languages implement two operators for performing bit shifts. Given a bit string and a number n, the left bit shift << will shift a bitstring n bits to the left. If the appending a 0 byte in the least significant (leftmost) position each shift. For programming languages where the underlying data type of the bit string has a fixed byte length, a left bit shift will discard the most significant (right most) bit in the string. The following example is a bit shift executed on an unsigned 4 bit number.
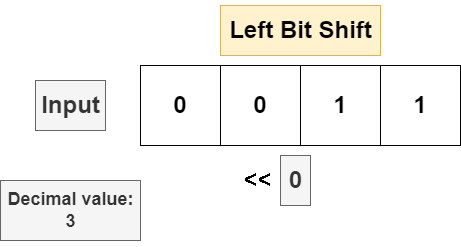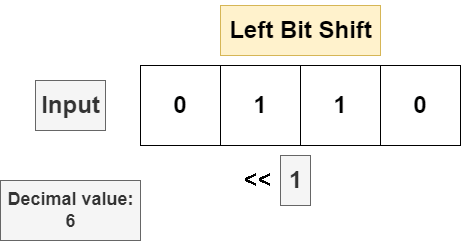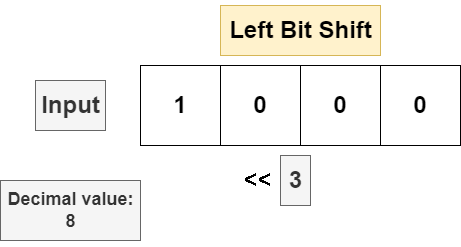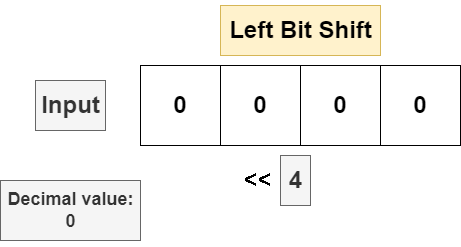
The right bit shift will move every bit in the string n bits to the right, discarding the least significant bit in the bit string and appending a 0 in the most significant position. If the input bit string is a signed data type and the sign bit is set to 1 (meaning the input is negative), then some implementations will insert a 1 in the most significant position to leave the operand negative, but this is not universal. The following is a bit shift on an unsigned 4 bit number.
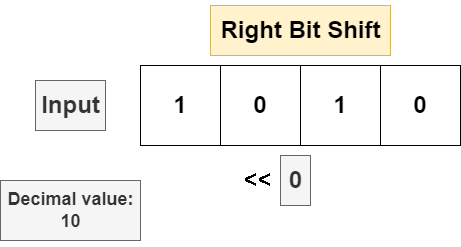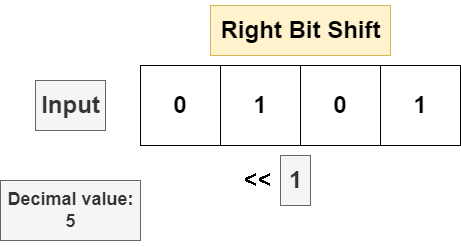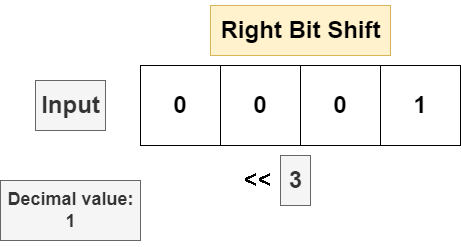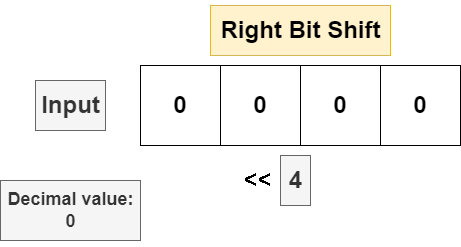
Bit shifting is implemented with the << (for left shift) and >> (for right shift) operators:
a = 0b110
print(bin(a >> 2))
b = 0b1
print(bin(b << 3))0b1 0b1000
Try it yourself!
| Output: | ||||
| Operation: | ||||
| Display: |
Applications of bitwise operations
Operations on bit-based data structures
Many data structures can be represented purely as a string of bits, meaning that they can easily be manipulated by bitwise operations. The the most notable examples of bit-level data structures are bit fields and bitmaps, and both representations are easily modifiable and queryable via bitwise operations. To see how bitwise operations can be leveraged to manipulate and get information on bit fields, see our article on them.
Optimizing multiplication with bit shifts
In many cases, bitwise operations can be significantly faster ways to perform certain mathematical operations instead of standard arithmetic at the CPU instruction level. Many compilers take advantage of this idea, and will have compiled binaries execute bit shifts instead of multiplication operations where doing so would optimize program runtime. In specific, we can take advantage of the idea that a left bit shift is the same as multiplying by 2 to speed up our program. Let's consider a small C program running on an x86 instruction set:
int a = 2;
a = a * 16;At first guess, we would expect this program to execute some multiplication instruction (in the case of x86, the instruction would be mul or imul), but if we decompile the binary of this program with objdumb -d, we can see that our program is actually using shl (x86's left bit shift instruction) to do the multiplication!
0000000000001129 <main>:
1129: f3 0f 1e fa endbr64
112d: 55 push %rbp
112e: 48 89 e5 mov %rsp,%rbp
1131: c7 45 fc 02 00 00 00 movl $0x2,-0x4(%rbp) ; int a = 2 occurs here.
1138: c1 65 fc 04 shll $0x4,-0x4(%rbp) ; left shift executed here!
113c: b8 00 00 00 00 mov $0x0,%eax
1141: 5d pop %rbp
1142: c3 retq
1143: 66 2e 0f 1f 84 00 00 nopw %cs:0x0(%rax,%rax,1)
114a: 00 00 00
114d: 0f 1f 00 nopl (%rax)The reason why our program ultimately uses shll instead of simply multiplying the two numbers is because x86's bit shift instruction runs significantly faster than a multiplication instruction. The compiler leverages the fact that we can very easily multiply a by 16 by instead bit shifting it by 4 instead, and runs the faster instruction.
That said, using bit shifts in high-level source code generally does not provide a unique performance boost. For compiled languages, what instructions the CPU executes is determined by the compiler, and the level and form of optimization can vary wildly depending system architecture and the specific compiler that is used. In practical terms, this means that using bit shifts over multiplication is a readability concern instead of a performance concern, and programmers should not use bit shifts in place of multiplication to achieve performance.